Uji Lanjut Anova Dua Jalur adalah pengujian lanjut dari Anova Dua Jalur yang dilakukan untuk mengetahui letak perbedaan hipotesis yang di uji secara signifikan . Berikut ini adalah makalah tentang Uji Lanjut Anova Dua Jalur yang kami buat untuk memenuhi tugas mata kuliah Metode Statistika I :
Read More → Uji Lanjut Anova Dua Jalur
Thursday, May 30, 2013
Analisis Variansi Dua Jalur
Analisis Variansi Dua jalur digunakan untuk menguji hipotesis perbandingan lebih dari dua sampel dan setiap sampel terdiri atas dua jenis atau secara bersama-sama. Berikut ini adalah makalah tentang Anova Dua Jalur yang kami buat untuk memenuhi tugas mata kuliah Metode Statistika I :
Read More → Analisis Variansi Dua Jalur
Uji Lanjut Anova Satu Jalur
Uji Lanjut Anova Satu Jalur adalah pengujian lanjut dari Anova Satu Jalur yang dilakukan untuk mengetahui letak perbedaan hipotesis yang di uji secara signifikan . Berikut ini adalah makalah tentang Uji Lanjut Anova Satu Jalur yang kami buat untuk memenuhi tugas mata kuliah Metode Statistika I :
Read More → Uji Lanjut Anova Satu Jalur
Analisis Variansi Satu Jalur
Analisis Variansi Satu Jalur adalah pengujian yang membandingkan lebih dari dua rata-rata sedangkan gunanya untuk menguji kemampuan generalisasi. Jika terbukti berbeda berarti kedua sampel tersebut dapat digeneralisasikan (data sampel dianggap dapat mewakili [populasi]). Berikut ini adalah makalah tentang Anova Satu Jalur yang kami buat untuk memenuhi tugas mata kuliah Metode Statistika I :
Read More → Analisis Variansi Satu Jalur
Uji Hipotesis Dua Rata - Rata
Pengujian Hipotesis Dua Rata - Rata adalah pengujian hipotesis terhadap statistik beda rata - rata sampel untuk membuat kesimpulan parameter beda rata - rata populasi. Berikut ini adalah makalah tentang uji Hipotesis Dua Rata - Rata yang kami buat untuk memenuhi tugas mata kuliah Metode Statistika I :
Read More → Uji Hipotesis Dua Rata - Rata
Thursday, May 16, 2013
Memanfaatkan Internet untuk Belajar Bilangan Bulat
Salah satu kegunaan internet adalah sebagai penyedia sumber belajar. Berikut ini adalah contoh Rencana Pelaksanaan Pembelajaran (RPP) Matematika materi Bilangan Bulat untuk kelas 7 SMP semester I :
Standar Kompetensi :
1. Memahami sifat-sifat operasi hitung bilangan dan penggunaannya dalam pemecahan masalah.
Kompetensi Dasar :
1.1. Melakukan operasi hitung bilangan bulat
Indikator :
1. Memberikan contoh bilangan bulat.
2. Menentukan letak bilangan bulat pada garis bilangan.
3. Melakukan operasi hitung bilangan bulat.
A. Tujuan Pembelajaran
1. Siswa dapat memberikan contoh bilangan bulat.
2. Siswa dapat menentukan letak bilangan bulat pada garis bilangan.
3. Siswa dapat melakukan operasi hitung pada bilangan bulat.
B. Materi Ajar
• Garis bilangan dan operasi hitung bilangan bulat
C. Alokasi Waktu : 2 X 45 menit (1 kali pertemuan).
D. Metode Pembelajaran :
Metode : Kooperatif menggunakan Internet
Pendekatan : Konstruktivisme
E. Langkah-langkah Kegiatan Pembelajaran
1. Kegiatan pembelajaran dapat diawali dengan memanfaatkan video YouTube berkaitan dengan bilangan bulat.
Dengan video yang berdurasi 8 menit 17 detik , memberikan ilustrasi secara nyata tentang bilangan bulat , khususnya operasi hitung bilangan bulat .
2. Setelah mengajak siswa menonton video yang berkaitan dengan bilangan bulat dan operasi hitungnya, kemudian guru memberikan umpan balik kepada siswa dengan mengajukan pertanyaan-pertanyaan yang mengarahkan siswa untuk mengingat apa yang mereka dapatkan dari video tersebut . Misalnya :
a. Kepingan warna hitam dilambangkan sebagai apa ?
b. Kepingan warna merah dilambangkan sebagai apa ?
c. Bagaimana operasi penjumlahan bilangan positif dan negatif ?
dan lain sebagainya .
3. Selanjutnya guru meminta siswa untuk membentuk kelompok kecil lalu berdiskusi mengenai video tersebut dan menemukan konsepnya sendiri .
4. Setelah berdiskusi, guru dapat mengajak siswa bermainan kuis matematika yang berkaitan dengan materi ini . Dapat di temukan di ixl.com atau www.thatquiz.org .
F. Alat / Bahan dan Sumber Belajar
• Buku Pelajaran Matematika untuk SMP Kelas 7 khususnya materi Bilangan Bulat . Atau dapat juga di download disini
Latihan Soal :
Read More → Memanfaatkan Internet untuk Belajar Bilangan Bulat
Standar Kompetensi :
1. Memahami sifat-sifat operasi hitung bilangan dan penggunaannya dalam pemecahan masalah.
Kompetensi Dasar :
1.1. Melakukan operasi hitung bilangan bulat
Indikator :
1. Memberikan contoh bilangan bulat.
2. Menentukan letak bilangan bulat pada garis bilangan.
3. Melakukan operasi hitung bilangan bulat.
A. Tujuan Pembelajaran
1. Siswa dapat memberikan contoh bilangan bulat.
2. Siswa dapat menentukan letak bilangan bulat pada garis bilangan.
3. Siswa dapat melakukan operasi hitung pada bilangan bulat.
B. Materi Ajar
• Garis bilangan dan operasi hitung bilangan bulat
C. Alokasi Waktu : 2 X 45 menit (1 kali pertemuan).
D. Metode Pembelajaran :
Metode : Kooperatif menggunakan Internet
Pendekatan : Konstruktivisme
E. Langkah-langkah Kegiatan Pembelajaran
1. Kegiatan pembelajaran dapat diawali dengan memanfaatkan video YouTube berkaitan dengan bilangan bulat.
Dengan video yang berdurasi 8 menit 17 detik , memberikan ilustrasi secara nyata tentang bilangan bulat , khususnya operasi hitung bilangan bulat .
2. Setelah mengajak siswa menonton video yang berkaitan dengan bilangan bulat dan operasi hitungnya, kemudian guru memberikan umpan balik kepada siswa dengan mengajukan pertanyaan-pertanyaan yang mengarahkan siswa untuk mengingat apa yang mereka dapatkan dari video tersebut . Misalnya :
a. Kepingan warna hitam dilambangkan sebagai apa ?
b. Kepingan warna merah dilambangkan sebagai apa ?
c. Bagaimana operasi penjumlahan bilangan positif dan negatif ?
dan lain sebagainya .
3. Selanjutnya guru meminta siswa untuk membentuk kelompok kecil lalu berdiskusi mengenai video tersebut dan menemukan konsepnya sendiri .
4. Setelah berdiskusi, guru dapat mengajak siswa bermainan kuis matematika yang berkaitan dengan materi ini . Dapat di temukan di ixl.com atau www.thatquiz.org .
F. Alat / Bahan dan Sumber Belajar
• Buku Pelajaran Matematika untuk SMP Kelas 7 khususnya materi Bilangan Bulat . Atau dapat juga di download disini
Latihan Soal :
Tuesday, May 7, 2013
Barisan
Barisan bilangan didefinisikan sebagai susunan bilangan yang memiliki pola atau aturan tertentu antara satu bilangan dengan bilangan berikutnya. Barisan terbagi menjadi dua jenis, yaitu :
1. Barisan Aritmatika
2. Barisan Geometri
• Barisan Aritmatika
Barisan aritmetika adalah suatu barisan dimana selisih atau beda dua suku yang berurutan konstan (tetap).
Misal:
1) 3, 7, 11, 15, 19, …
2) 30, 25, 20, 15, 10, …
Perhatikan bahwa selisih di antara suku-sukunya selalu tetap. Barisan yang demikian itu disebut barisan aritmetika. Selisih itu disebut beda suku atau beda saja dan dilambangkan dengan c.
Barisan l) mempunyai beda, b = 4. Barisan ini disebut barisan aritmetika naik karena nilai suku-sukunya makin besar.
Barisan 2) mempunyai beda, b = -5. Barisan ini disebut barisan aritmetika turun karena nilai suku-sukunya makin kecil.
Rumus suku ke n :
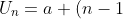b)
Rumus beda :
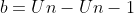
• Barisan Geometri
Barisan Geometri adalah suatu barisan dengan pembanding (rasio) antara dua suku yang berurutan selalu tetap . Bentuk umum :
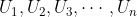 atau
atau
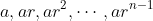
Jika kita memulai barisan geometri dengan suku pertama a dan rasio r , maka kita mendapatkan barisan berikut :

Jadi, disebut barisan geometri jika
disebut barisan geometri jika 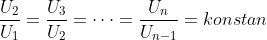
Kontansta ini disebut pembanding atau rasio (r)
Rumus Rasio :
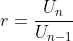
Rumus Suku ke n :
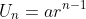
Read More → Barisan
1. Barisan Aritmatika
2. Barisan Geometri
• Barisan Aritmatika
Barisan aritmetika adalah suatu barisan dimana selisih atau beda dua suku yang berurutan konstan (tetap).
Misal:
1) 3, 7, 11, 15, 19, …
2) 30, 25, 20, 15, 10, …
Perhatikan bahwa selisih di antara suku-sukunya selalu tetap. Barisan yang demikian itu disebut barisan aritmetika. Selisih itu disebut beda suku atau beda saja dan dilambangkan dengan c.
Barisan l) mempunyai beda, b = 4. Barisan ini disebut barisan aritmetika naik karena nilai suku-sukunya makin besar.
Barisan 2) mempunyai beda, b = -5. Barisan ini disebut barisan aritmetika turun karena nilai suku-sukunya makin kecil.
Rumus suku ke n :
Rumus beda :
• Barisan Geometri
Barisan Geometri adalah suatu barisan dengan pembanding (rasio) antara dua suku yang berurutan selalu tetap . Bentuk umum :
Jika kita memulai barisan geometri dengan suku pertama a dan rasio r , maka kita mendapatkan barisan berikut :
Jadi,
Kontansta ini disebut pembanding atau rasio (r)
Rumus Rasio :
Rumus Suku ke n :
Sunday, May 5, 2013
Teorema Phytagoras
 Teorema Pythagoras menyatakan bahwa:
Teorema Pythagoras menyatakan bahwa:Jumlah luas bujur sangkar pada kaki sebuah segitiga siku-siku sama dengan luas bujur sangkar di hipotenus.
Sebuah segitiga siku-siku adalah segitiga yang mempunyai sebuah sudut siku-siku; kaki-nya adalah dua sisi yang membentuk sudut siku-siku tersebut, dan hipotenus adalah sisi ketiga yang berhadapan dengan sudut siku-siku tersebut.
Pythagoras menyatakan teorema ini dalam gaya goemetris, sebagai pernyataan tentang luas bujur sangkar: Jumlah luas bujur sangkar biru dan merah sama dengan luas bujur sangkar ungu.
Akan halnya, Sulbasutra India juga menyatakan bahwa :
Tali yang direntangkan sepanjang panjang diagonal sebuah persegi panjang akan menghasilkan luas yang dihasilkan sisi vertikal dan horisontalnya. Menggunakan aljabar, kita dapat mengformulasikan ulang teorema tersebut ke dalam pernyataan modern dengan mengambil catatan bahwa luas sebuah bujur sangkar adalah pangkat dua dari panjang sisinya:
Jika sebuah segitiga siku-siku mempunyai kaki dengan panjang a dan b dan hipotenus dengan panjang c, maka a+ b' = c
Java applet ini menunjukkan suatu segitiga siku-siku. Anda dapat menggerakkan titik sudut siku-siku segitiga dengan menekan dan menggerakkan tomobol pada mouse.
| a2 = c p |
| b2 = c q |
| a2 + b2 = c2 |
URL: http://www.walter-fendt.de/m14id/pyththeorem_id.htm
© Walter Fendt, November 1, 1997
© Translation: Zulkardi 2000
Last modification: November 14, 2005
© Walter Fendt, November 1, 1997
© Translation: Zulkardi 2000
Last modification: November 14, 2005
GeoGebra
Apa itu GeoGebra ?
Read More → GeoGebra
GeoGebra
adalah software yang dapat dijadikan alat bantu dalam pembelajaran matematika
yang bersifat dinamis dan interaktif untuk mendukung pembelajaran dan
penyelesaian soal-soal matematika khususnya Geometri, Aljabar dan Kalkulus.
GeoGebradikembangkan oleh Markus Hohenwarter yang berasal dari Austria. Dengan
GeoGebra kita bisa membuat sebuah kontruksi titik yang berupa Point, Vektor,
Segmentasi ataupun Garis termasuk dengan fungsinya. Selain itu GeoGebra juga
memiliki kemampuan untuk menggunakan variable dengan angka, vektor dan titik,
menemukan turunan dan integral fungsi dan lain-lainnya. Tentunya GeoGebra dapat
pula digunakan untuk menyelesaikan dan menggambarkan berbagai persoalan
matematika yang lebih kompleks .
Ingin
bermain GeoGebra secara online?
Silahkan coba
dibawah ini :
|
Ranni Permatasari, 3 May 2013, Created with GeoGebra |
Friday, May 3, 2013
Aritmatika Sosial
Dalam kehidupan sehari-hari , kita sering kali melakukan aplikasi dari materi Aritmatika Sosial , misalnya dalam hal berbelanja . Tapi tahukah kalian bagaimana cara menghitung harga-harga dari penjualan , pembelian , untung , rugi, dan diskon .
Coba perhatikan video dibawah ini , simak baik-baik , lalu kalian akan menemukan semua rumusnya dari pemahaman pada video ini .
Next Video :
The last video :
Setelah menonton 3 video diatas , kalian dapat menemukan rumus-rumus menghitung harga penjualan , pembelian , untung , rugi , dan diskon . Sehingga kalian bisa menghitung sendiri harga-harga ketika kalian belanja .
Semoga bermanfaat :)
Read More → Aritmatika Sosial
Coba perhatikan video dibawah ini , simak baik-baik , lalu kalian akan menemukan semua rumusnya dari pemahaman pada video ini .
Next Video :
The last video :
Setelah menonton 3 video diatas , kalian dapat menemukan rumus-rumus menghitung harga penjualan , pembelian , untung , rugi , dan diskon . Sehingga kalian bisa menghitung sendiri harga-harga ketika kalian belanja .
Semoga bermanfaat :)
Bangun Datar
Read More → Bangun Datar
Subscribe to:
Comments (Atom)


